Step 6: Generate and Encode the Signature
When signing a transaction input, we follow these steps:
- Create an ECDSA signature using the private key and commitment hash
- Ensure it has a low S value (BIP62)
- Encode it in DER format
- Append the SIGHASH_ALL byte (0x01)
Let's use these values from our test vector:
| Value | Hex |
|---|---|
| Private Key | 619c335025c7f4012e556c2a58b2506e30b8511b53ade95ea316fd8c3286feb9 |
| Public Key | 025476c2e83188368da1ff3e292e7acafcdb3566bb0ad253f62fc70f07aeee6357 |
| Commitment Hash | c37af31116d1b27caf68aae9e3ac82f1477929014d5b917657d0eb49478cb670 |
Step 1: ECDSA Signature Generation
The ECDSA algorithm signs our commitment hash using the private key to generate a signature. The signature consists of two values (r, s):
# 1. Create signing key from private key bytes
sk = SigningKey.from_string(private_key, curve=SECP256k1)
# 2. Generate deterministic signature (RFC 6979)
signature_der = sk.sign_digest_deterministic(
commitment,
hashfunc=hashlib.sha256,
sigencode=util.sigencode_der)
# 3. Decode signature to get r and s values
r, s = util.sigdecode_der(signature_der, SECP256k1.order)Our test vector generates:
r: 3609e17b84f6a7d30c80bfa610b5b4542f32a8a0d5447a12fb1366d7f01cc44a
s: a8c56ab3bae7ccea9ebf906fcff170cb61b9c3bddb0c7f1133238e5ee9b75553Step 2: Low S Value Check
In ECDSA, there are actually two valid S values for every signature: a "high" and a "low" value.
Both are mathematically valid, but Bitcoin requires using the low S value to prevent transaction malleability.
Curve Order (N) = FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
N/2 = 7FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF5D576E7357A4501DDFE92F46681B20A0If S > N/2, we must use (N - S) as the new S value. This prevents anyone from modifying our transaction's signature (and thus its TXID) after broadcast while keeping it valid.
# Check if s is high (BIP62)
if s > SECP256k1.order // 2:
# Convert to low-s
s = SECP256k1.order - s
# Re-encode with low-s
signature_der = util.sigencode_der(r, s, SECP256k1.order)Our test vector generates:
s: a8c56ab3bae7ccea9ebf906fcff170cb61b9c3bddb0c7f1133238e5ee9b75553
n - s: 573a954c4518331561406f90300e8f3358f51928d43c212a8caed02de67eebee (low s value)We choose n - s because it's the lower value, making our signature BIP62 compliant.
Step 3: DER Encoding
The signature must be encoded in DER format with this structure:
0x30 [Total Length]
0x02 [Length of R]
[R value]
0x02 [Length of S]
[S value]Our test vector encoded:
30 - Sequence marker
44 - Total remaining length
02 - Integer marker for R
20 - Length of R (32 bytes)
3609e17b84f6a7d30c80bfa610b5b4542f32a8a0d5447a12fb1366d7f01cc44a - R value
02 - Integer marker for S
20 - Length of S (32 bytes)
573a954c4518331561406f90300e8f3358f51928d43c212a8caed02de67eebee - S valueStep 4: Add SIGHASH Byte
Finally, we append the SIGHASH_ALL byte (0x01):
Final Signature: 304402203609e17b84f6a7d30c80bfa610b5b4542f32a8a0d5447a12fb1366d7f01cc44a0220573a954c4518331561406f90300e8f3358f51928d43c212a8caed02de67eebee01Notice that while we used 4 bytes for SIGHASH_ALL (00000001) when creating the commitment hash, we only append 1 byte (01) to the final signature. This is intentional:
- The 4-byte value is committed to in the hash we sign
- The 1-byte value indicates how to interpret the signature This prevents anyone from changing the SIGHASH type after the fact, as it would invalidate the signature.
Complete Code Implementation
def sign(private_key: bytes, commitment: bytes) -> bytes:
# Create signing key from private key bytes
sk = SigningKey.from_string(private_key, curve=SECP256k1)
while True:
# Create deterministic signature (RFC 6979)
signature_der = sk.sign_digest_deterministic(
commitment,
hashfunc=hashlib.sha256,
sigencode=util.sigencode_der
)
# Decode signature to get r and s values
r, s = util.sigdecode_der(signature_der, SECP256k1.order)
# Check if s is high (BIP62)
if s > SECP256k1.order // 2:
# Convert to low-s
s = SECP256k1.order - s
# Re-encode with low-s
signature_der = util.sigencode_der(r, s, SECP256k1.order)
# Add SIGHASH_ALL byte
signature_with_sighash = signature_der + b'\x01'
# Only exit if we have low-s
if s <= SECP256k1.order // 2:
break
return signature_with_sighashTest Vector
Let's verify again our implementation against the official BIP143 test vectors.
def test_signature():
# Private key from BIP143 test vector
privkey = bytes.fromhex(
'619c335025c7f4012e556c2a58b2506e30b8511b53ade95ea316fd8c3286feb9'
)
# Commitment hash from previous step
commitment = bytes.fromhex(
'c37af31116d1b27caf68aae9e3ac82f1477929014d5b917657d0eb49478cb670'
)
# Generate signature
signature = sign(privkey, commitment)
# Expected signature from BIP143
expected_sig = bytes.fromhex(
'304402203609e17b84f6a7d30c80bfa610b5b4542f32a8a0d5447a12fb1366d7f01cc44a' +
'0220573a954c4518331561406f90300e8f3358f51928d43c212a8caed02de67eebee01'
)
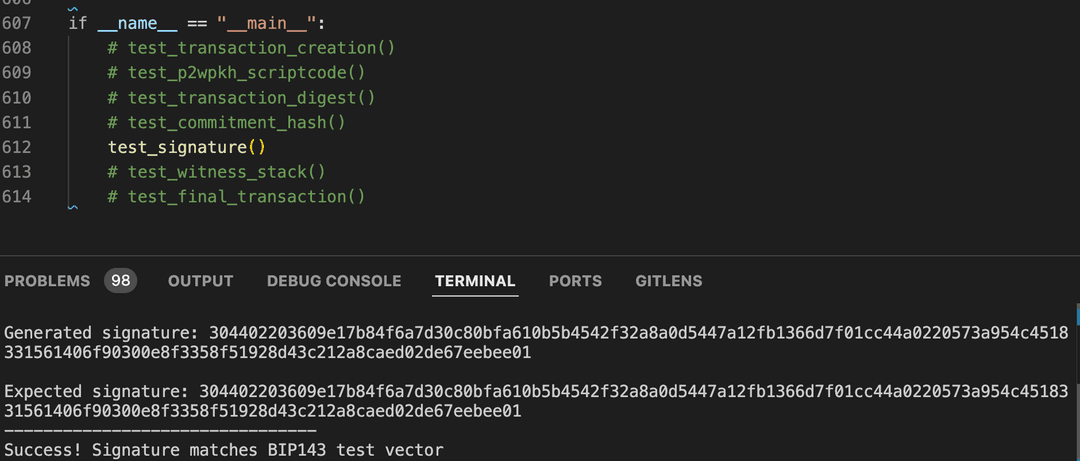
print("Generated signature:", signature.hex())
print("Expected signature:", expected_sig.hex())
assert signature == expected_sig, "Signature does not match BIP143 test vector"
print("Success! Signature matches BIP143 test vector")When you run this code locally, it will generate the exact signature from the BIP143 test vector .
# Expected signature from BIP143
signature = "304402203609e17b84f6a7d30c80bfa610b5b4542f32a8a0d5447a12fb1366d7f01cc44a0220573a954c4518331561406f90300e8f3358f51928d43c212a8caed02de67eebee01"Note about Browser Execution
This code cannot be run directly in the browser as Trinket doesn't support the ECDSA module. Please run the code locally to verify the signature generation. Here's what you should see when running locally:
Next Step
With our signature ready, we'll move on to adding the witness to our transaction.