MuSig
By the end of this article, we want Alice, Bob, and Carol to sign a transaction using MuSig.
We will explain step by step using both theory and code. Your task by the end is to write the code for this signature generation.
1. Theory
To make this article simple to follow, we will answer three important questions that will help you understand the concept: What? Why? How?
What is MuSig?
MuSig is simply a protocol for aggregating public keys and signatures.
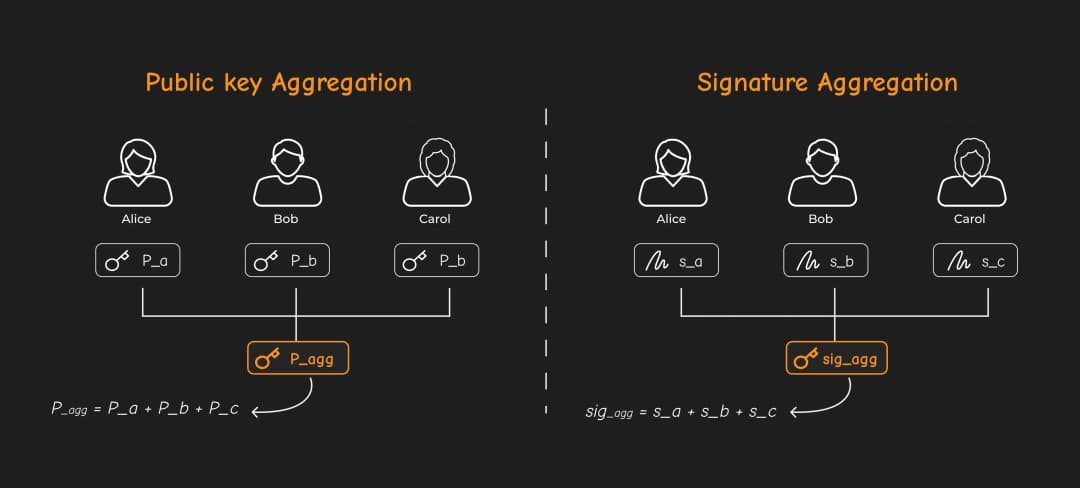

Why do we need MuSig?
The reasons we use MuSig are:
Transaction Size/Fees: MuSig makes multi-sig look like single-sig. This means you pay the same fees whether one person or ten people sign.
Privacy: Nobody can tell if a transaction used multiple signers or just one. Your multi-sig setup stays private, as it looks identical to a regular transaction.


How does MuSig work?
Now we need your focus here, please. Grab a coffee, and let's dive in.
Alice, Bob, and Carol want to create an aggregated signature such as:
To create this signature, we need to go through three main steps:
- Aggregating public keys.
- Aggregating nonces.
- Aggregating the signature.
Some of these steps require rounds of communication between participants:
- Aggregating public keys does not require communication.
- Aggregating nonces and signatures requires three rounds of communication (MuSig2 optimizes this to two rounds).


Step 1: Public Key Aggregation (Offline Process)
A naive way to do public key aggregation is by summing up each participant's public key:
However, this approach is vulnerable to a key cancellation attack.
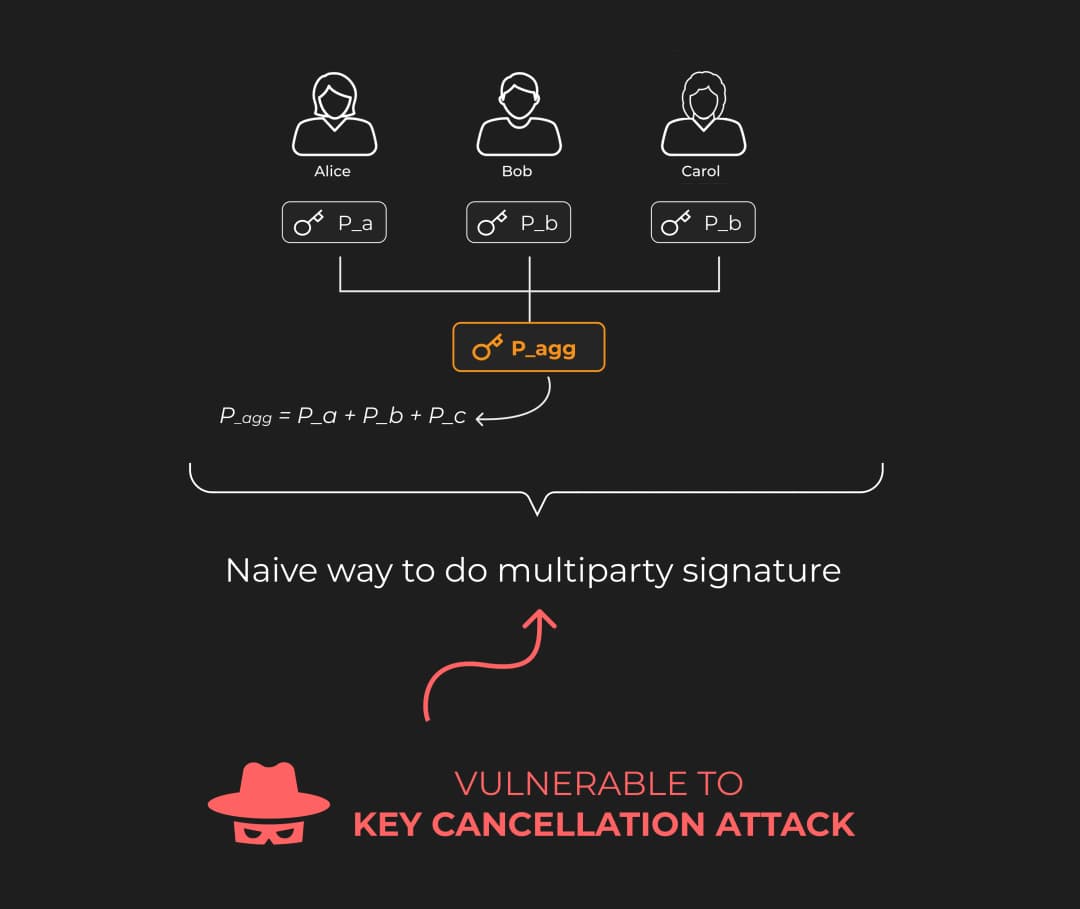

What is a key cancellation attack?
Imagine a scenario where Alice and Bob want to create a 2-of-2 aggregated signature.
How do we counteract the key cancellation attack?
To counteract this, we add a challenge factor to each participant's public key:
The challenge factor is generated based on the participants' aggregated public key.
This ensures that no individual participant can create a public key that offsets the public keys of others.
Here’s how we construct individual public keys and the aggregated public key:
(Remember, all of this happens offline. There’s no need for communication; public keys can be exchanged through offline channels.)


Exercise 1: Compute 3-of-3 MuSig public key
In this exercise, we'll use the generate_musig_key(pubkey_list) function to generate challenge factors for each participant and an aggregate MuSig pubkey.
generate_musig_key(pubkey_list) takes a list of the participants' public keys generate_musig_key([ECPubKey0, ECPubKey1, ...]) and returns a challenge map and the aggregate pubkey:
- The challenge map contains
ECPubKey_i, challenge_data_ikey - value pairs. - The aggregate pubkey is an
ECPubKeyobject.
Solution code
Now, let’s move to the next step: Aggregate Nonce.
Step 2: Aggregate Nonce (1st and 2nd Round of Communication)
The process of aggregating nonces is as follows:
- Alice, Bob, and Carol each generate a random nonce kA, kB, and kC.
- They calculate their respective nonce points: RA = kA * G, RB = kB * G, RC = kC * G.
- They exchange these nonce points (RA, RB, and RC).
- Finally, they calculate the aggregated nonce: Ragg = RA + RB + RC
Where do the rounds of communication happen in this process?
Great question! The process of aggregating nonces is somewhat similar to aggregating public keys.
Except: Public keys (e.g., PA, PB, and PC) stay the same for every signature process, but random numbers (kA, kB, kC) must change with every signature.
Thus, in each signature process, we need a round of communication where Alice, Bob, and Carol exchange their Ri values to construct: Ragg = RA + RB + RC
However, before this step (where they exchange Ri), there is a prior round of communication to ensure none of them cheats by changing their Ri after seeing the others’ values.
How do we prevent cheating?
To prevent cheating, Alice, Bob, and Carol must first exchange the hashes of their nonce points (e.g., H(RA), H(RB), H(RC)) before revealing their actual Ri values. This ensures that once they reveal their Ri, they cannot modify their values after seeing others’.
Summary: Two Rounds of Communication for Nonce Aggregation
Exchange hash commitments: Alice, Bob, and Carol share H(RA), H(RB), and H(RC).
Exchange nonce points: They reveal RA, RB, and RC.
Once all Ri values are shared, they compute the aggregated nonce: Ragg = RA + RB + RC
Exercise 2: Compute 3-of-3 MuSig nonce
In this exercise, we'll generate nonces for individual participants, calculate the nonce point commitments, and then generate an aggregate nonce point.
Solution code
Step 3: Signature Aggregation (Final Step)
After computing the aggregate public key (P_agg) and aggregate nonce (R_agg), each participant calculates their partial signature:
Where:
k_i: Participant's random nonce.d_i: Participant's private key.H: Hash function withR_agg,P_agg, and the messagem.
Aggregating the Signatures
Participants exchange their s_i values, and the aggregate signature is computed as:
s_agg = s_A + s_B + s_C
This simplifies to:
Where:
k_agg = k_A + k_B + k_C(aggregate nonce scalar).d_agg = d_A + d_B + d_C(aggregate private key scalar).
Final Signature
The final aggregate signature is:
(Ragg, s agg)
This pair can be verified using Pagg and the message m.
Exercise 3: Compute aggregated MuSig signature
In this exercise, we'll generate nonces for individual participants, calculate the nonce point commitments, and then generate an aggregate nonce point.
Solution code